Code

During my graduate course in dynamical systems, I explored the Takens theory of phase space reconstruction. Takens (1981) outlines a method for determining whether or not a set of data can be attributed to a strange attractor. By time sampling the data, one can create a phase space diagram that, for systems governed by a strange attractor, forms a distinctive torus like shape. With proper selection of the number of dimensions and time sampling interval, this method works even for noisy systems.

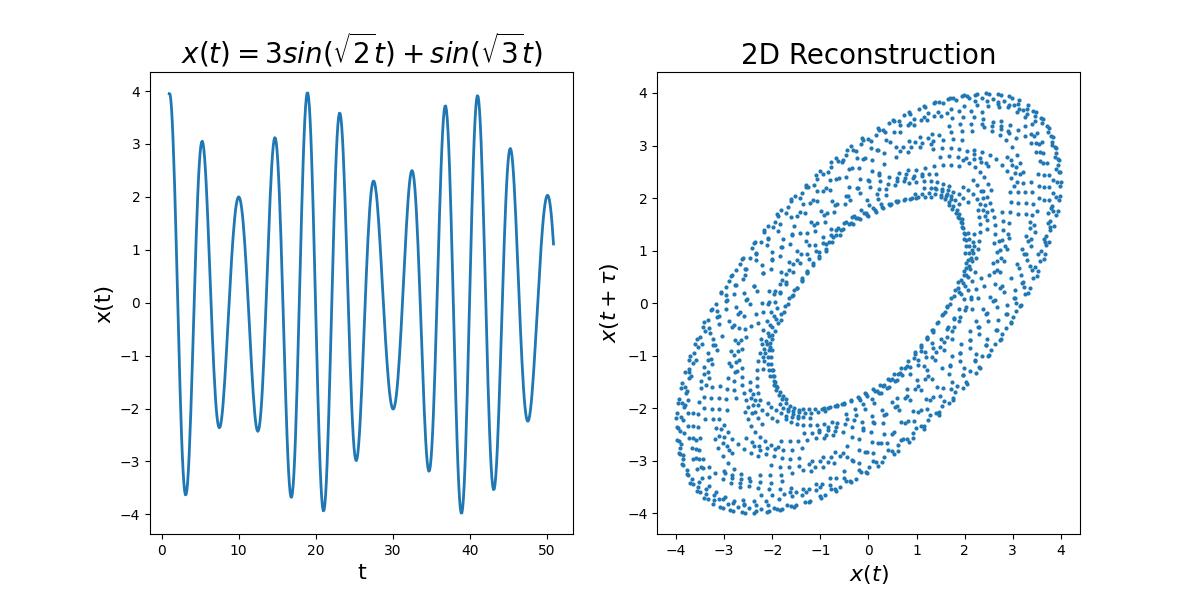
Above is a simple phase space reconstruction for a nonchaotic system. The Takens reconstruction method also works for complicated systems, see below.

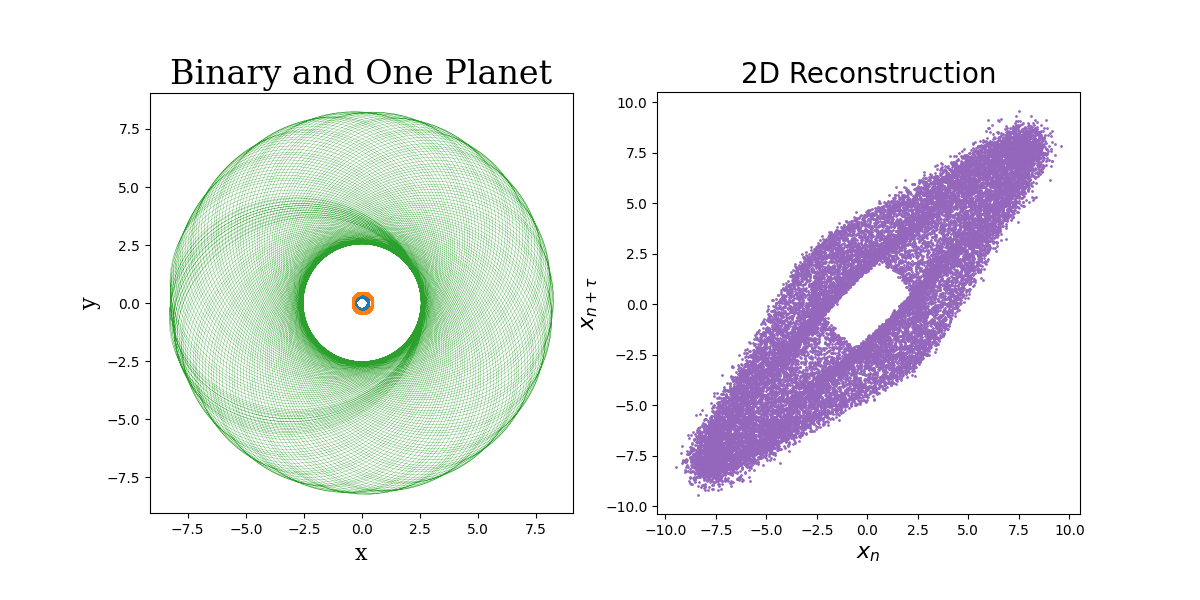
Above we have the phase space reconstruction of an N-body system made up of two "stars," heavier objects, and one "planet," a lighter object. After simulation, gaussian noise was added to the data. Again, the Takens reconstruction produces an open shape, but due to the complexity of the system and added noise, this shape is not as perfectly circular as with the simpler system.

As part of my work at the Southern California Earthquake Center, I implemented hierarchical matrices into a simulation of earthquakes and aseismic slip (SEAS) that included off- fault viscoelastic effects. Hierarchical matrices provide an approximation to a matrix vector product, reducing computation time from O(n^2) to O(nlogn).

In this project, hierarchical matrices were implemented using Michael Bradley's code dc3dm which allowed the interfacing of Matlab and C++.

I made a simple n-body simulation in python for a computational physics course at UCSC. The goal of my project was to explore the stability of eccentric orbits around a stable stellar binary, as a function of the semi major axis and eccentricity of the planet's orbit. Given that the simulation is coded in Python, it is pretty slow, but provided some nice insight and was useful in the above Takens reconstruction project. Below is an image demonstrating the stability (or lack thereof) of a planet orbitting a binary at different starting locations.